并查集

1. 介绍

并查集（英文：Disjoint-set data structure，直译为不交集数据结构）是一种数据结构，用于处理一些不交集（Disjoint sets，一系列没有重复元素的集合）的合并及查询问题。支持以下操作：

• 查询
  • 查询某个元素属于哪个集合，通常是返回集合内的一个“代表元素”
  • 这个操作是为了判断两个元素是否在同一个集合之中
• 合并
  • 将两个集合合并为一个
• 添加
  • 添加一个新集合，其中有一个新元素
  • 添加操作不如查询和合并操作重要，常常被忽略

2. 实现

2.1 表示

• 并查集中的每一个集合用树表示
• 一个节点是一个元素，保存着其父节点的引用
• 根节点的父指针指向其自身

class UnionFind {
  constructor (n) {
    /**
     * n 个元素的集合，使用 parent 数组存储其父指针。
     * 数组下标表示元素节点，下标索引对应的值表示元素的父节点
     *   - 如 [0, 0, 1] 表示 0 是树的根节点，1 的父节点是 0，2 的父节点是 1。
     *   - 这样也能推断出来，0 和 2 是连通关系
     * */
    this.parent = new Array(n).fill(0).map((item, index) => index)
  }
}

上述表示方法，并查集的元素数量在一开始就确定好了。如果想在初始化之后自由添加元素，就不能使用数组结构了。可以考虑使用其它数据结构管理并查集。

2.2 查找

查找即是查询元素所在集合的根节点。从x开始，根据节点到父节点的引用向根行进，直到找到根节点。

find(x) {
  if (this.parent[x] === x) return x;
  return find(this.parent[x]);
}

上述算法效率很差，如果树是链式结构，则复杂度高达 O(n)。一个优化方式就是路径压缩：在查询过程中，把所有子节点的父指针都直接指向根节点。

find(x) {
  if (this.parent[x] === x) return x;

  this.parent[x] = this.find(this.parent[x])
  return this.parent[x]
}

2.3 合并

初始化时，各元素之间相互独立，不存在连接关系。合并操作能够把两个元素所在集合合并为一个。思路是分别找到两个元素的根节点，并把其中一个根节点的父指针指向另一个根节点。

union(x, y) {
  const xRoot = this.find(x);
  const yRoot = this.find(y);

  if (xRoot !== yRoot) {
    this.parent[xRoot] = yRoot;
  }
}

上述代码的问题在于，它直接把 x 集合挂到 y 集合的根节点上了。可能会使生成的新树不够平衡，深度过大。虽然经过路径压缩后，深度不成为问题，但数量多的树指向数量少的树时，要改变父指针的节点变多了。

一个能简单想到的优化思路是合并时，比较两集合的大小，用数量少的树指向数量多的树。

另一个优化思路是按秩合并，其计算规则如下：

• 只有根节点的树（即只有一个元素的集合），秩为0；
• 当两棵秩不同的树合并后，新的树的秩为原来两棵树的秩的较大者；
• 当两棵秩相同的树合并后，新的树的秩为原来的树的秩加一。

与按数量合并相比，秩的数量范围更小，也更容易维护。

class UnionFind {
  constructor(n) {
    this.parent = new Array(n).fill(0).map((item, index) => index)

    // 默认每个元素的初始秩为 0
    this.rank = new Array(n).fill(0);
  }

  union(x, y) {
    const xRoot = this.find(x);
    const yRoot = this.find(y);
  
    if (xRoot !== yRoot) {
      // 按秩合并
      if (this.rank[xRoot] < this.rank[yRoot]) {
        this.parent[xRoot] = yRoot;
      } else if (this.rank[xRoot] > this.rank[yRoot]) {
        this.parent[yRoot] = xRoot;
      } else {
        // 秩相同时，统一指向 y，并更新其秩
        this.parent[xRoot] = yRoot;
        this.rank[yRoot]++
      }
    }
  }  
}

3. 实战——以岛屿数量 (opens new window)为例

3.1 读题

3.1.1 原题

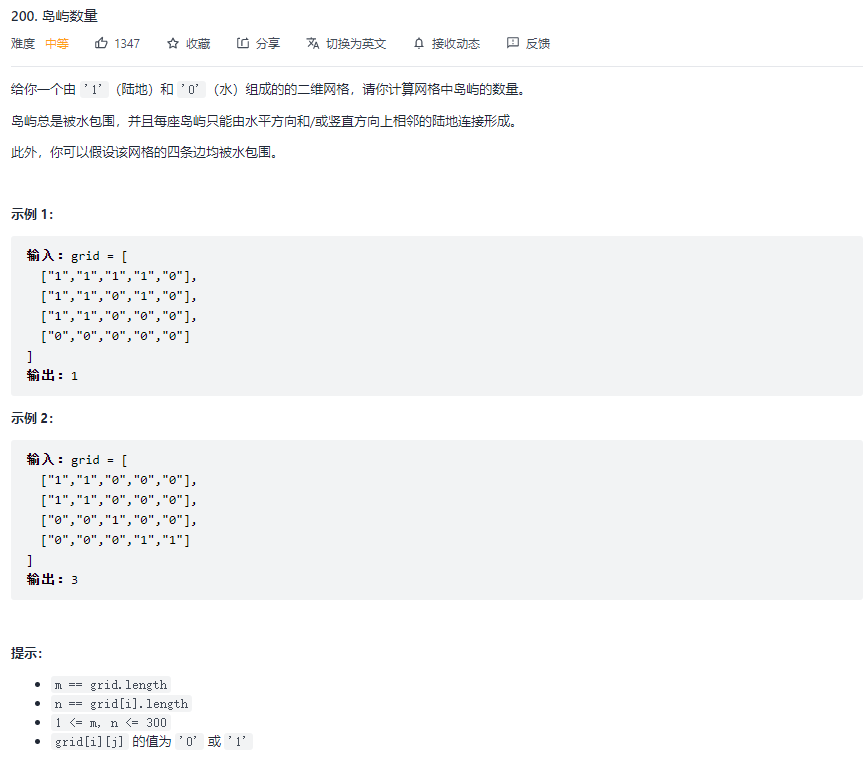
3.1.2 分析

要计算岛屿数量，实际上就是判断有哪些节点连接在一起。

3.2 并查集的实现

let numIslands = grid => {
  const m = grid.length;
  const n = grid[0].length;

  const uf = new UnionFind(m * n);
  for (let i = 0; i < m; i++) {
    for (let j = 0; j < n; j++) {
      if (grid[i][j] !== '1') continue;


      let curIdx = i * n + j;
      uf.init(curIdx);
      // 向右连接
      if (j < n - 1 && grid[i][j + 1] === '1') {
        uf.union(curIdx, curIdx + 1);
      }

      // 向下连接
      if (i < m - 1 && grid[i + 1][j] === '1') {
        uf.union(curIdx, curIdx + n);
      }
    }
  }

  return uf.count()
}

并查集的实现：

class UnionFind {
  constructor(n) {
    this.parent = new Array(n).fill(0).map(_ => -1);
    this.rank = new Array(n).fill(0);
  }

  find(x) {
    if (this.parent[x] !== x) {
      this.parent[x] = this.find(this.parent[x]);
    }

    return this.parent[x];
  }

  union(x, y) {
    this.init(x);
    this.init(y);

    const parentX = this.find(x);
    const parentY = this.find(y);

    if (parentX === parentY) return;

    let diff = this.rank[parentX] - this.rank[parentY];
    if (diff < 0) {
      this.parent[parentX] = parentY;
    } else if (diff > 0) {
      this.parent[parentY] = parentX;
    } else {
      this.parent[parentX] = parentY;
      this.rank[parentY]++;
    }
  }

  // 初始化集合
  init(x) {
    if (this.parent[x] === -1) {
      this.parent[x] = x;
    }
  }

  // 获取集合个数
  count() {
    let set = new Set();

    for (let item of this.parent) {
      if (item === -1) continue;

      set.add(this.find(item));
    }

    return set.size();
  }
}

3.3 其它解法

因为本题中的元素是基于数组的，这种通常也可以使用深搜或广搜来实现。

3.3.1 深搜

let numIslands = grid => {
  const fn = (i, j) => {
    grid[i][j] = 0;

    // 向左
    if (j > 0 && grid[i][j - 1] === '1') fn(i, j - 1);
    // 向右
    if (j < n - 1 && grid[i][j + 1] === '1') fn(i, j + 1);
    // 向下
    if (i < m - 1 && grid[i + 1][j] === '1') fn(i + 1, j);
    // 向上
    if (i > 0 && grid[i - 1][j] === '1') fn(i - 1, j);
  }

  const m = grid.length;
  const n = grid[0].length;
  let count = 0;

  for (let i = 0; i < m; i++) {
    for (let j = 0; j < n; j++) {
      if (grid[i][j] === '1') {
        count++;
        fn(i, j);
      }
    }
  }

  return count;
}

3.3.2 广搜

numIslands = grid => {
  const m = grid.length;
  const n = grid[0].length;
  let count = 0;

  const queue = [];
  for (let i = 0; i < m; i++) {
    for (let j = 0; j < n; j++) {
      if (grid[i][j] === '1') {
        count++;
        queue.push([i, j]);
        grid[x][y] = '0';

        while (queue.length) {
          const [x, y] = queue.shift();

          grid[x][y] = '0';

          // 向上
          if (x > 0 && grid[x - 1][y] === '1') {
            grid[x - 1][y] = '0';
            queue.push([x - 1, y]);
          }
          // 向下
          if (x < m - 1 && grid[x + 1][y] === '1') {
            grid[x + 1][y] = '0';
            queue.push([x + 1, y]);
          }
          // 向左
          if (y > 0 && grid[x][y - 1] === '1') {
            grid[x][y - 1] = '0';
            queue.push([x, y - 1]);
          }
          // 向右
          if (y < n - 1 && grid[x][y + 1] === '1') {
            grid[x][y + 1] = '0';
            queue.push([x, y + 1]);
          }
        }
      }
    }
  }

  return count;
}