# 逻辑回归
# 1. 二分分类与逻辑回归
逻辑回归(Logistic Regression)是一种用于解决二分类(0 or 1)问题的机器学习方法,用于估计某种事物的可能性。
逻辑回归(Logistic Regression)与线性回归(Linear Regression)都是一种广义线性模型(generalized linear model),与线性回归有很多相同之处。逻辑回归假设因变量 y 服从伯努利分布,而线性回归假设因变量 y 服从高斯分布。
逻辑回归以线性回归为理论支持,通过 Sigmoid 函数引入非线性因素,以处理 0/1 分类问题。
因此去除 Sigmoid 映射函数的话,逻辑回归算法就是一个线性回归。
# 2. 逻辑回归
在二分分类问题中,目标是训练出一个分类器,以图片的特征向量 x 作为输入,预测输出的结果标签 y 是1 还是 0。
# 逻辑回归中的维度
- b 表示偏置量,为一个实数
- 向量化
# 3. 回归函数
使用线性回归函数可以拟合出特征与结果的映射关系:
由于逻辑回归是处理二分法问题的,其结果应在区间
sigmoid 函数图像如下:

# 4. 损失函数与成本函数
# 损失函数
所谓损失,就是预测值与真实值的偏离程度。损失越小,表示学习结果越好。
损失函数定义了回归在单个训练样本上的表现:

# 成本函数
损失函数只定义了回归在单个训练样本上的表现,成本函数则衡量了在全体训练样本上的表现,其计算公式为所有训练样本的损失值求平均:
# 5. 导数与梯度下降
成本函数
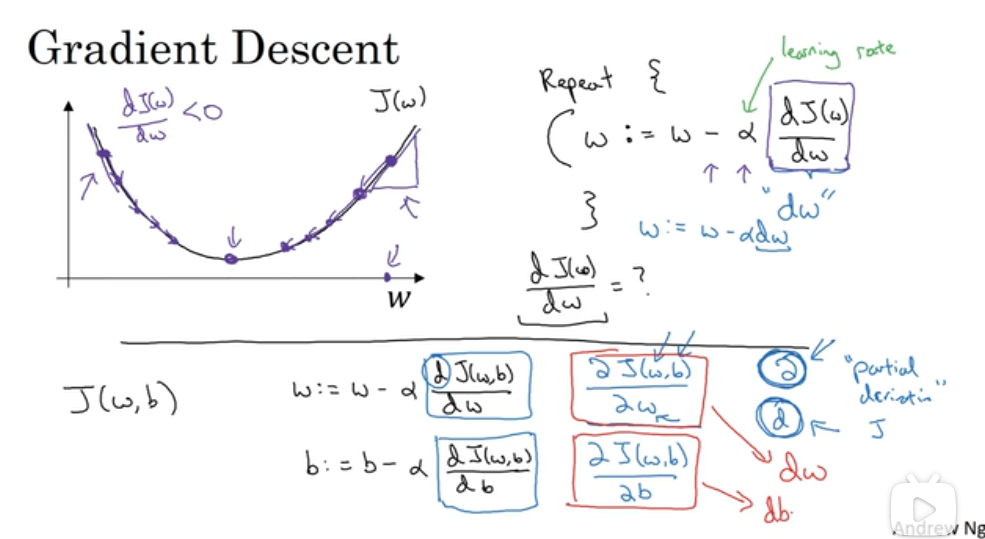
# 导数
导数就是斜率。
# 梯度下降法
# 计算图
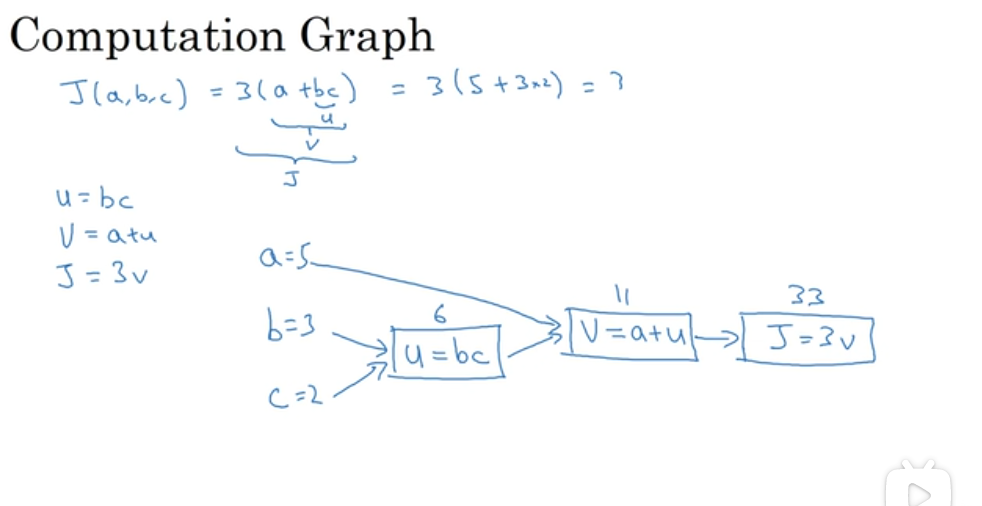
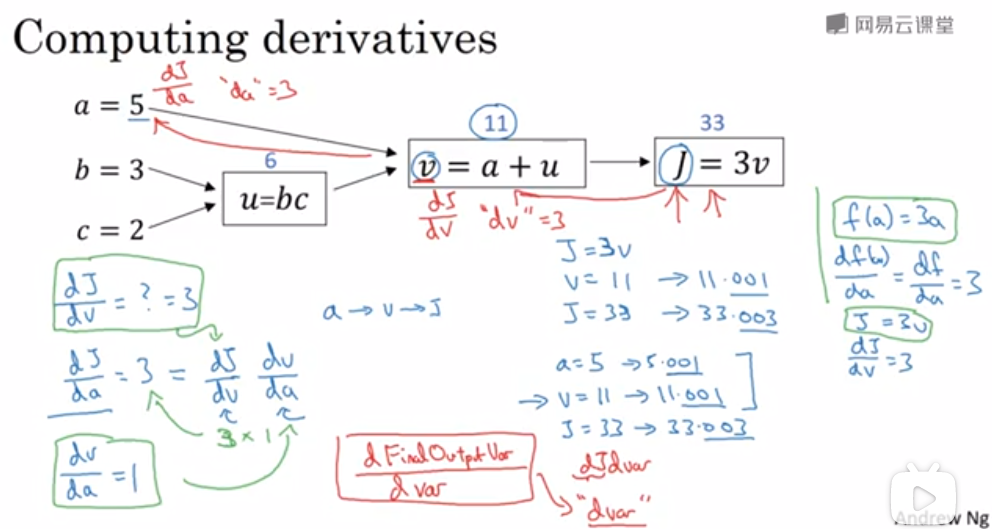
# 向后传播
# 逻辑回归的梯度下降
单个样本的梯度下降

m 个样本的梯度下降

