# 浅层网络
# 1. 神经网络概览
# 1.1 概览
对于单个神经元节点,具有输入、参数、输出。
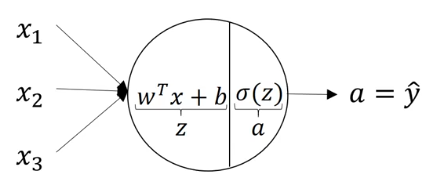
神经网络是对许多神经元节点的组合,每个节点独立的工作同它们单独执行的工作类似。
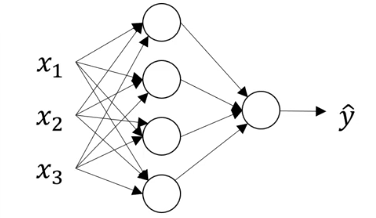
为了便于计算参数,会将其向量化,以层为单位,批量计算输出,更新参数集。
# 1.2 神经网络的表示
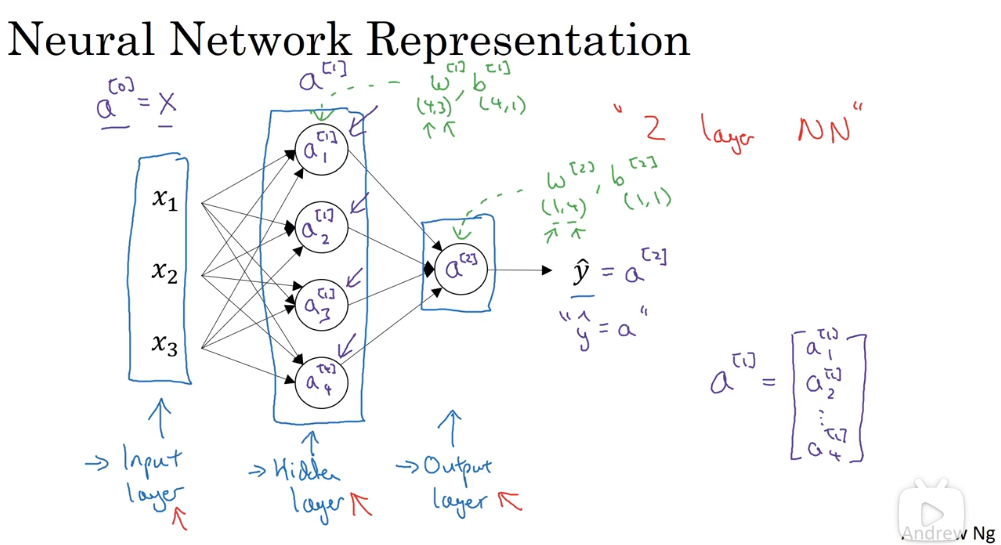
- 特征输入层:Input Layer
- 输入层与输出层中间的层级:Hidden Layer
- 隐藏层的含义是,在训练过程中,这些节点计算得到的结果我们是不知道的。
- 实际上,我们只是通过许多隐藏层叠加计算,得到输出结果,用成本函数反推来更新隐藏层的参数。我们并不关心隐藏层计算的结果。
- 可能有多个层
- 输出层:Output Layer
激活值表示该层最终传递给下一层的值。
# 1.3 符号约定
- 示例:
# 2. 神经网络的计算实现
# 2.1 参数的随机初始化
不能把参数都初始定义为 0,这样会导致同一层的所有隐藏节点计算同样的内容,进行同样的更新,失去了隐藏层多节点的作用。下图是证明:
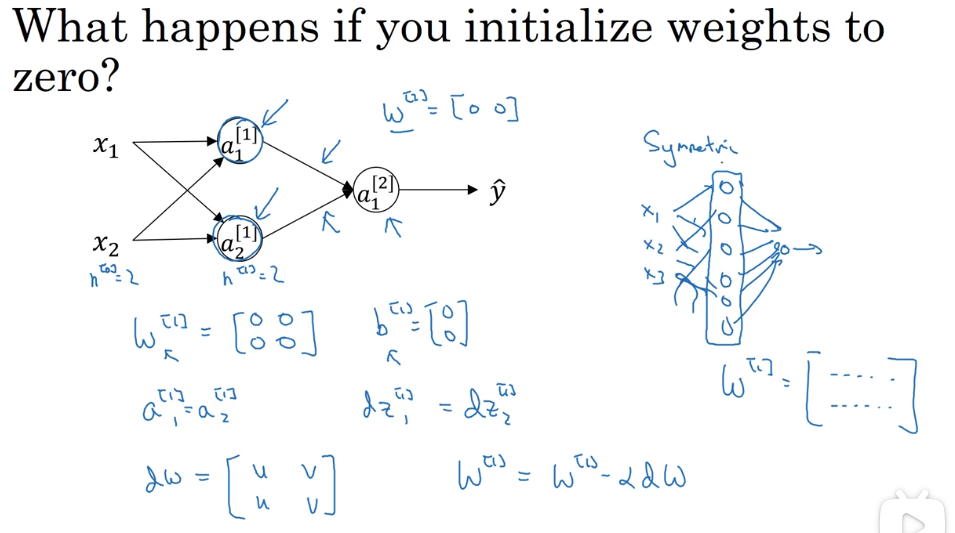
更好的方式是将其初始化为一个非常小的随机值:
非常小的原因是,避免其激活值落在非常大或非常小的区间,那里的导数很小,梯度下降法会非常慢,减小了学习速度。
至于偏置数 b,初始可以设为 0。
# 2.2 计算单个训练样本的输出
每个节点的输出计算公式如下:
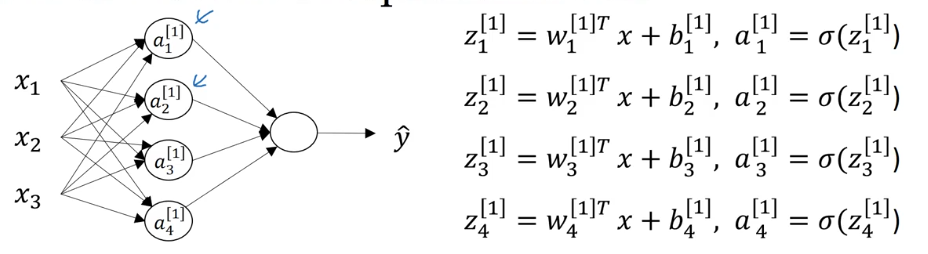
将其向量化:
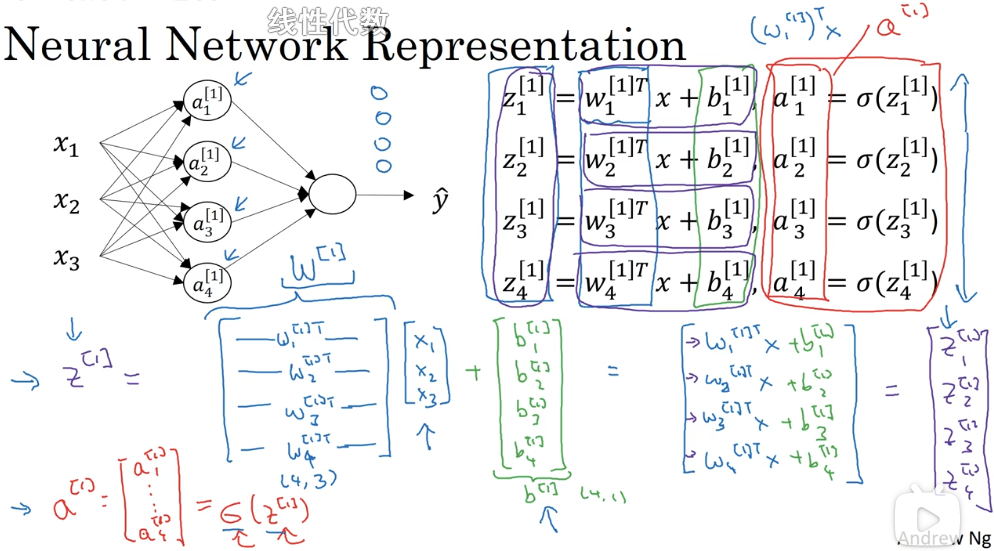
向量化之后,不再需要挨个节点计算 w、b,而是直接计算每层的输出:
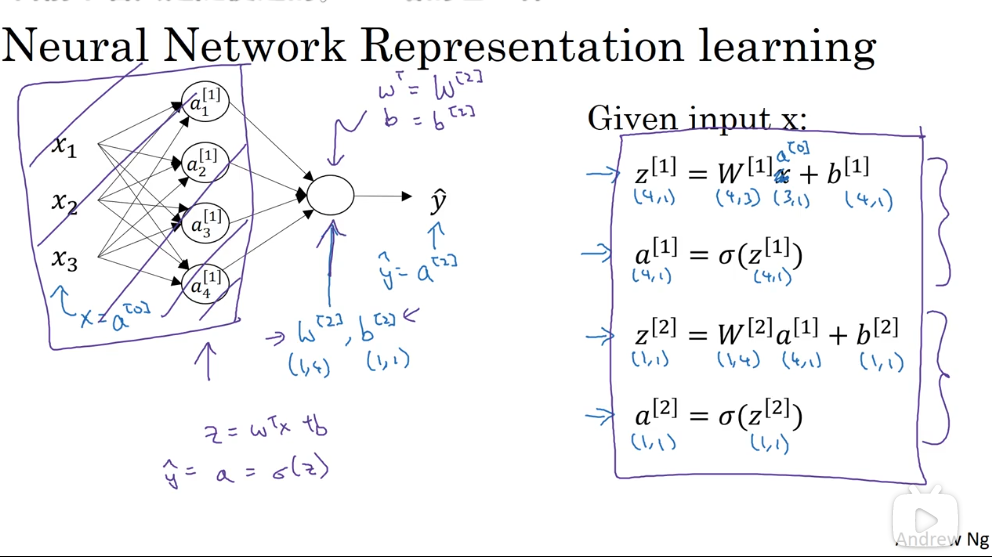
对于第 m 个样本,其最终的计算公式如下:
其中,
这里的向量化实际上是把一层中所有神经节点的参数向量化,由 $w^{[n]}_1, w^{[n]}_2, w^{[n]}_3, ... $ 变为
# 2.3 多个样本的向量化计算
上面解决了单个样本的结果计算问题,由于训练样本数量巨大,对于样本的循环计算仍旧是个代价很大的过程。
通过将样本集向量化,能够改善这一局面。
其原理性推导如下:
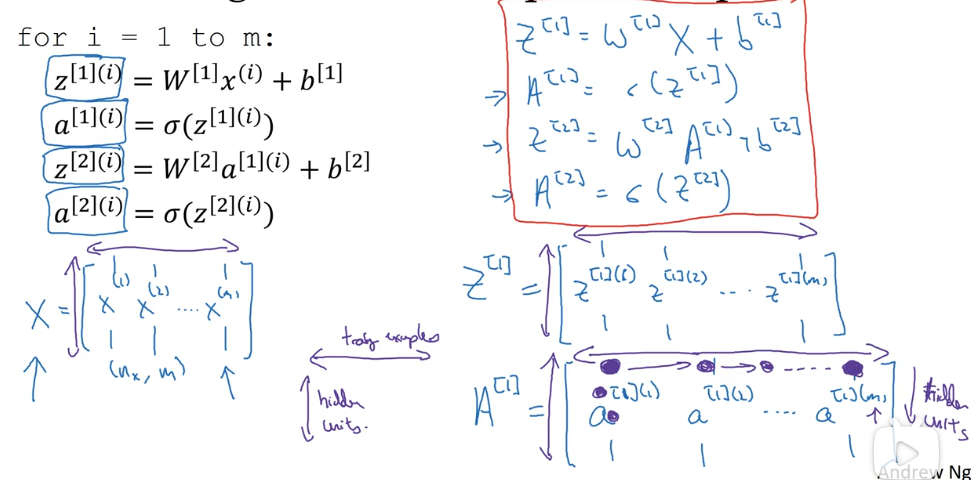
最终得到的计算公式为:
其中,
与 2.1 中的公式相比,似乎只是换了字母的大小写,实际上这种变化也意味着,每个变量指代的值由单个样本结果转变为多个样本结果,即
下图对公式(1)的正确性进行了更细致的证明:
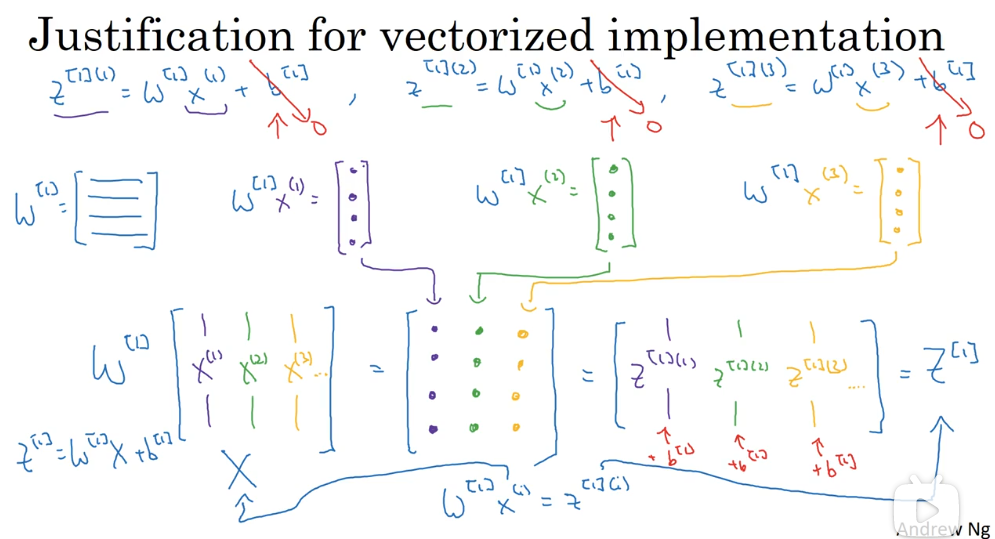
# 2.4 反向传播
梯度下降原理:

梯度下降是更新深度学习参数的一种方法,其理论基础是找到参数的成本函数,然后对各参数求偏导,使其朝向成本更小的方向更新,以找出使成本函数尽可能小的参数集。
根据前向传播的公式,得到反向传播的公式,这些公式是通过导数计算推导出来的:

成本函数:
计算导数:
更新参数:
其中,
# 3. 关于激活函数
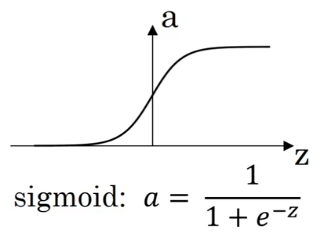
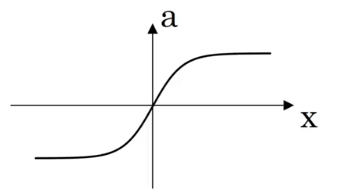
# 3.1 激活函数类型
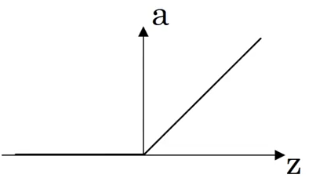
ReLU 函数的一个缺点是当值小于 0 时,斜率为 0。
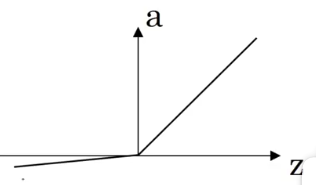
# 3.2 选择激活函数的一些经验法则
- 如果输出值是 0 和 1,
sigma 函数得到的结果介于 0 和 1 之间,而 tanh 函数的结果在 -1 和 1 之间,tanh 函数得到的值的平均分布更靠近 0,有类似数据中心化的效果,这使得下一层的学习更方便一点。所以 tanh 函数几乎在所有场合都比 sigma 函数更为优越。
sigma 和 tanh 函数共有的一个缺点是,如果 z 特别大或者特别小,那么激活函数的导数的梯度(亦即该函数的斜率)会变得很小,这会拖慢梯度下降算法。
深度学习的一个特点是,在建立神经网络时经常有很多不同的选择,如隐藏单元数、激活函数、权重的初始化等。很难有一个明确的准则,规定在解决问题时应该如何选择。
# 3.3 为什么激活函数都是非线性的
非线性激活函数的必要性:如果激活函数是线性的,那么多层网络就失去了意义,最终计算出的值只是特征的简单线性关系。

