# 深层神经网络
# 1. 概述
# 1.1 符号定义
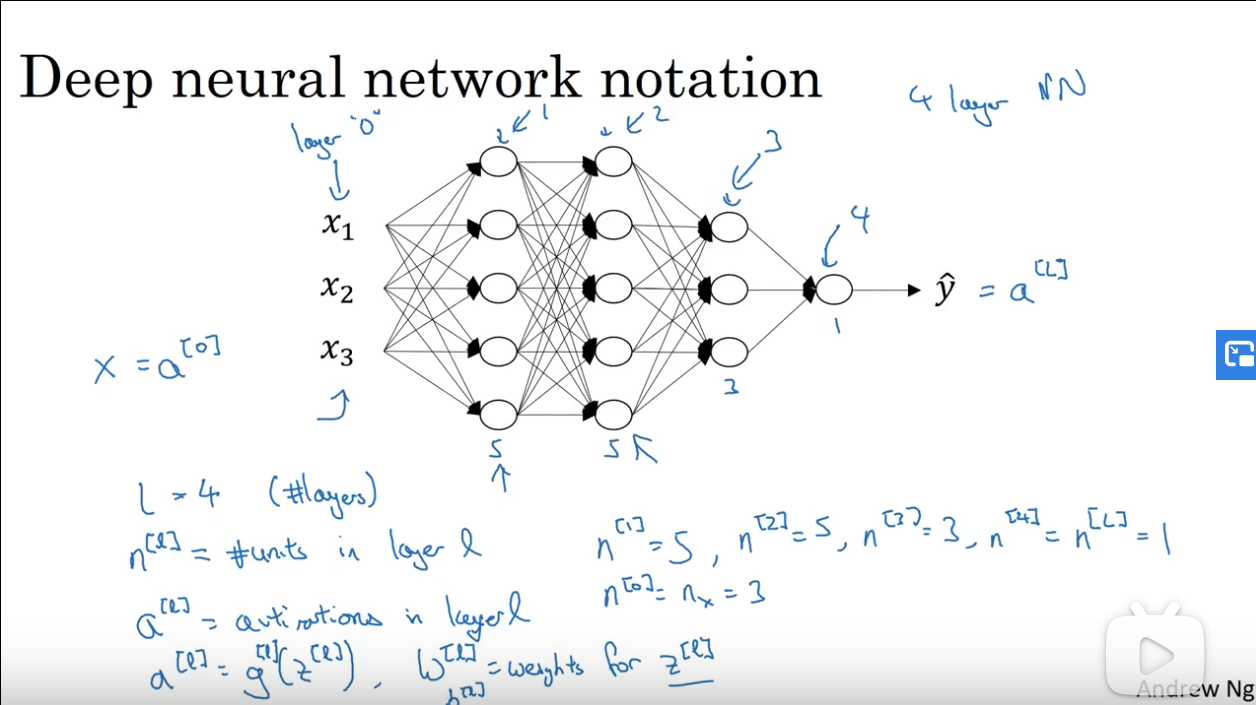
# 2. 深层网络的计算
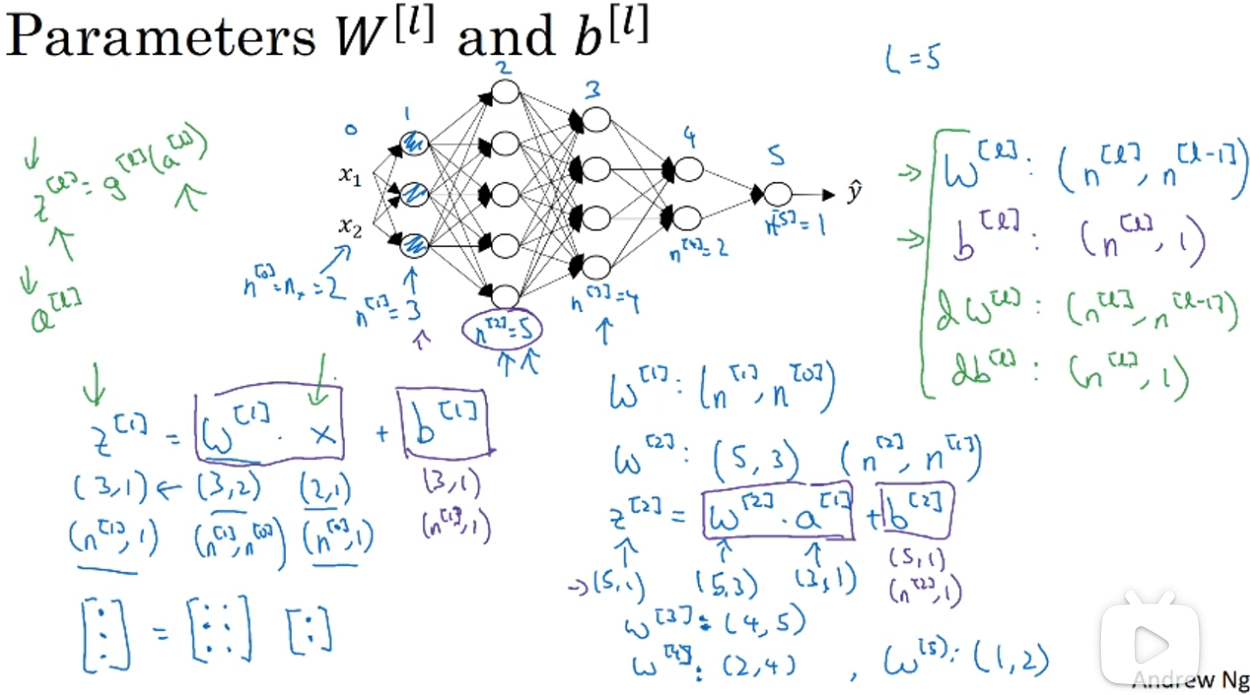
# 2.1 核对各层矩阵的维数
一种比较有效减少模型 bug 的方法,就是拿张纸过一遍算法中矩阵的维数。基本方法就是根据当前层所需结果反推参数矩阵的维数。
以
举例
归纳可得,
且 dW 的维度同 W,db 的维度同 b。
对于多个样本,向量化之后,
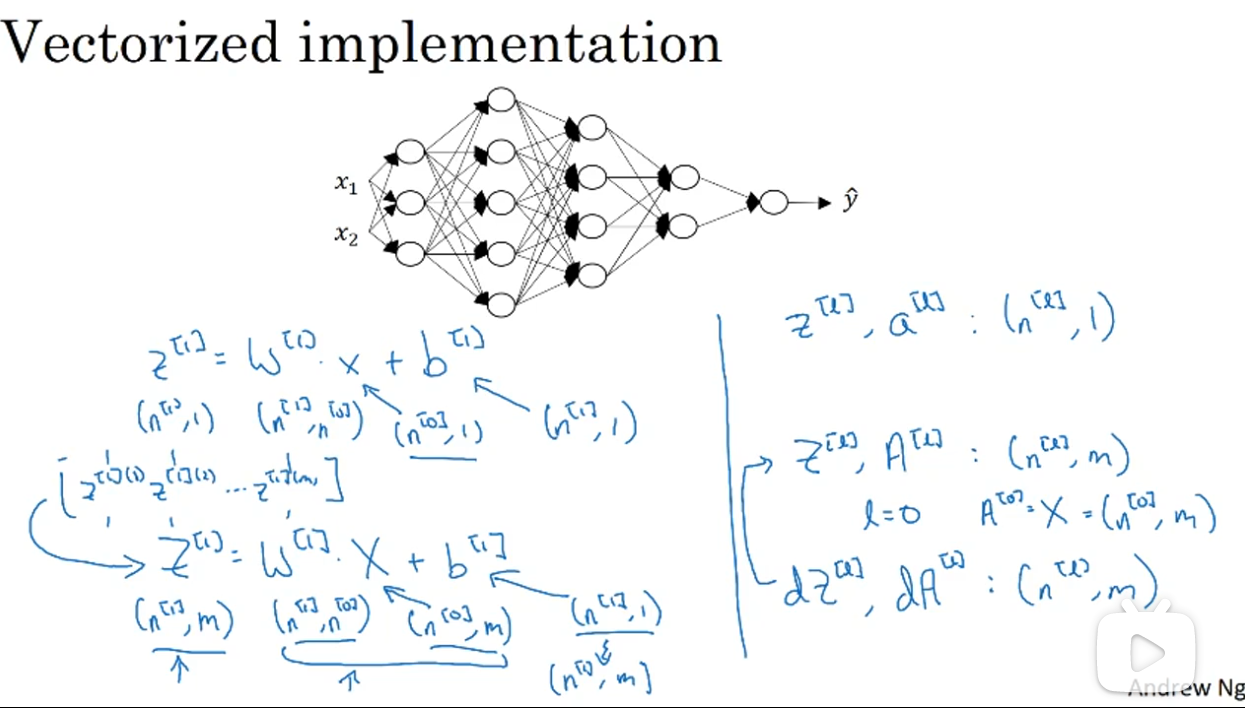
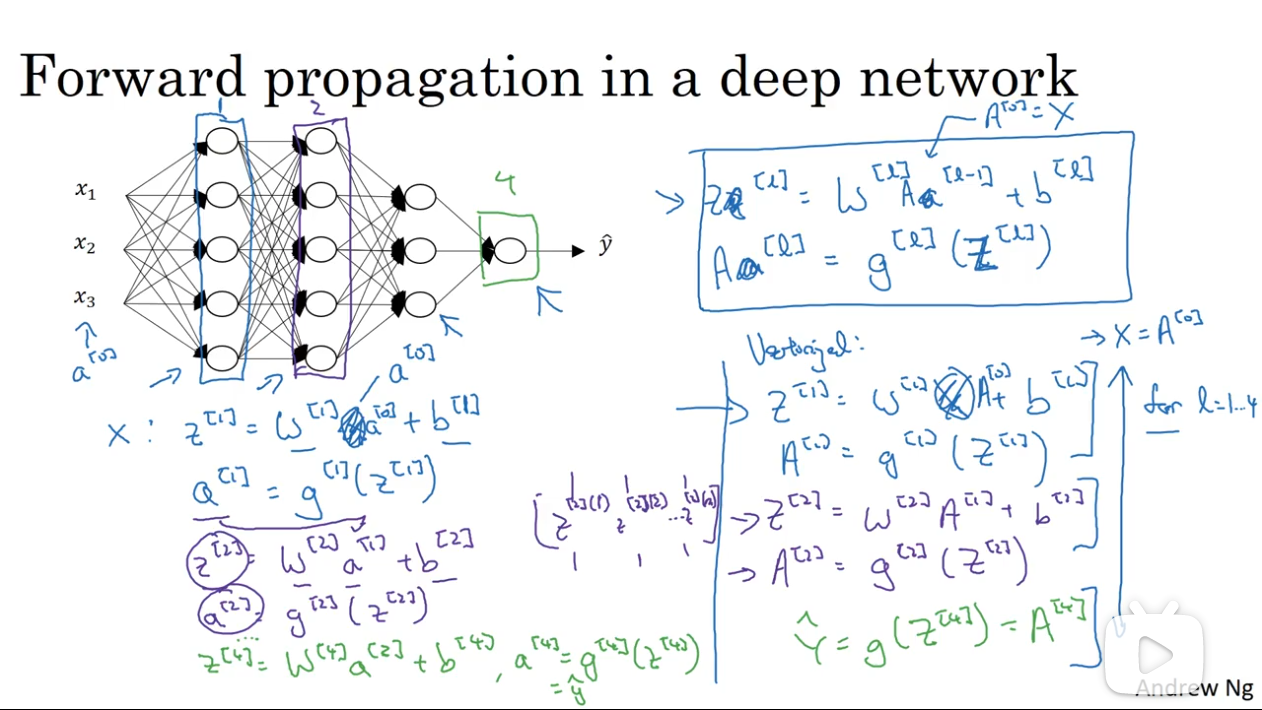
# 2.2 前向传播
对于正向传播,其输入输出如下:
- Input:
- Output:
- cache:
按照顺序,先计算前一层,然后再计算下一层。这里可以(大概也只能)使用显式的 for 循环。
# 2.3 反向传播
其输入输出如下:
- Input:
- Output:
传播公式如下:

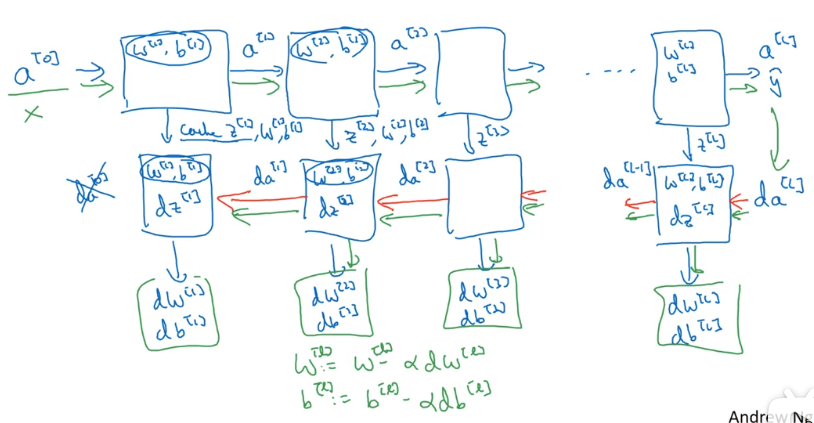
# 2.4 一次学习迭代的完整流程
一次完整的学习迭代是对数据集进行一次正向传播与反向传播,更新一次模型参数。其中所需的计算如下:
# 3. 深度学习中的参数与超参数
# 3.1 超参
深度学习模型中,除了训练所需的参数 W,b ,还有一些参数也需要输入模型之中:
- learning rate:
- iterations
- hidden layers
- hidden units
- choice of activation function
这些数据被称为超参数,因为这些数据如何设置,最终决定了参数 W 和 b 的学习结果。
# 3.2 超参的设置
当你自己着手于训练自己的深度神经网络时,你可能发现超参的选择上有很多可能性,所以你需要多做尝试。
今天的深度学习应用领域还是很经验性的过程。通常你有一个想法,比如可能大概知道一个较好的学习率是 0.01,然后你尝试一下。然后基于尝试的结果发现学习率的调整方向。
# 3. 为什么需要深层网络
其实深度学习的网络并不需要很大(即节点数不需要特别多),但是其中隐藏层最好多一些。
# 3.1 深层网络在构建什么
直觉上,可以把其浅层看作是探测一些低层级的简单特征,之后把它们在深层结合起来,以学习更复杂的特征,类似下面这种:
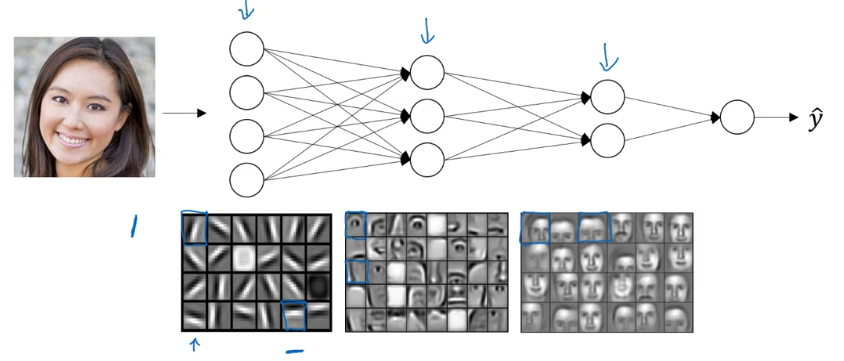
浅层可能学习一些图像的基本特征,如边缘。渐渐地组合出人脸的局部特征,如眼睛、鼻子等,进而识别出整张人脸。
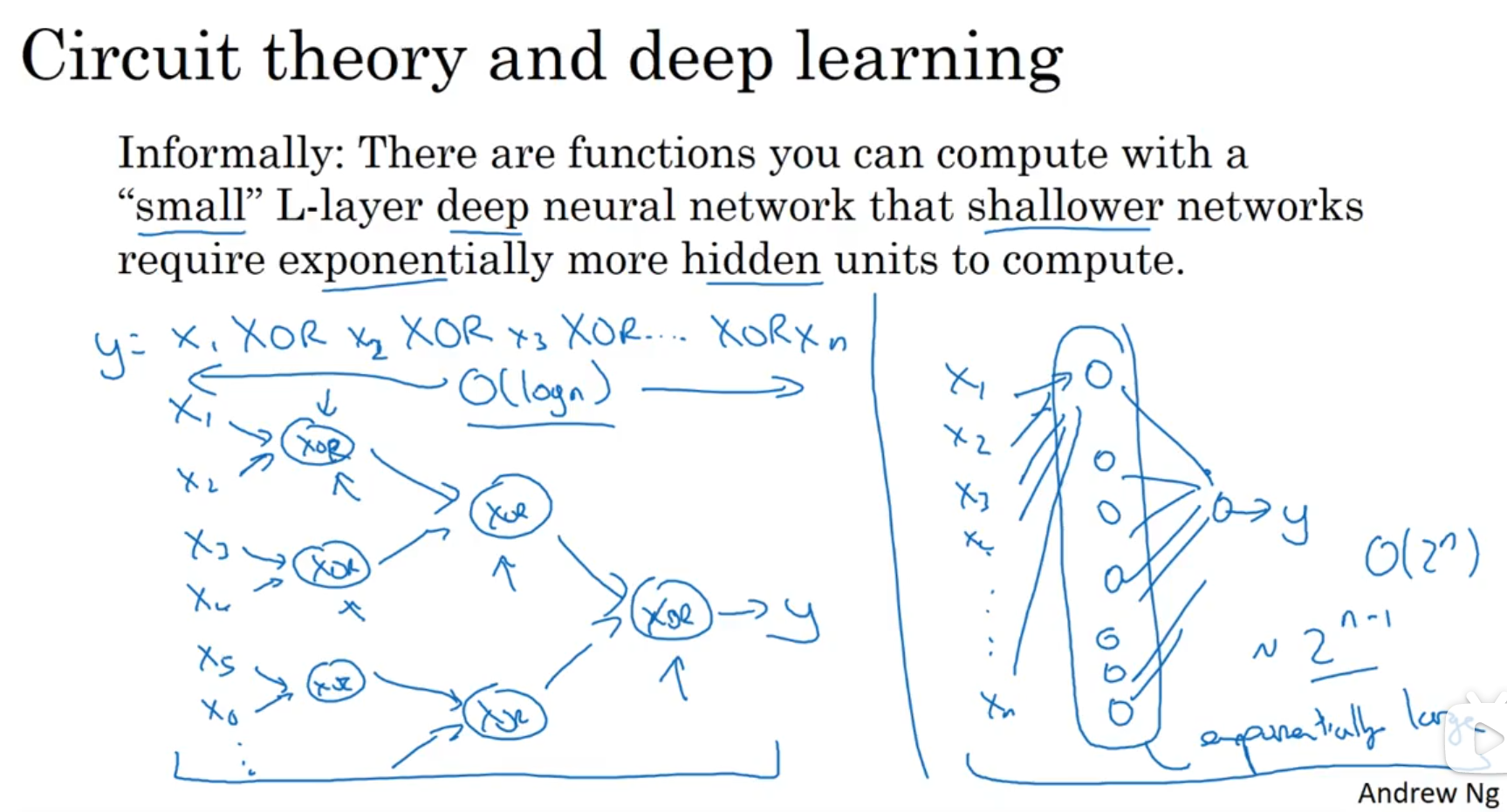
# 3.2 用电路理论来解释深层网络存在的意义
如果不扩展深度,而是增加单个层级的神经节点,那么最终会使得节点数成指数级增加。
# 4. 大佬的只言片语
我必须要说,即使到现在我在实现一个算法的时候,有时候我也会惊讶怎么莫名其妙就成功了。那是因为机器学习里的复杂性是来源于数据,而不是那一行行代码。
所以有时候你会感觉,你实现了几行代码,但是不太确定它具体做了什么,但是奇迹般地成功了。那其实是因为真正神奇的不是你写的程序,通常情况下你的代码段不会很长,虽然也不太简单,但至少不需要一万行代码。但有时当你喂入超多数据之后,就算我已经搞了好多年机器学习,有时还是会在算法管用的时候惊讶一下下。因为实际上你的算法的复杂性来源于数据,而不是你写的代码。
神经网络与大脑毫无关系。
