# 正则化
如果怀疑网络过拟合了数据,即存在高方差的情况,其中一个解决办法就是正则化。
当然,另一个方式就是准备更多数据,也很有用。
# 1. 什么是正则化
正则化在成本函数中添加了一个与 W 有关的项和超参。
# 逻辑回归中的正则化

其中,
# 神经网络中的正则化

正向传播的成本函数公式为:
其中,
# 使用该范数实现梯度下降
正则化对于模型的影响,就在于其参与了反向传播的过程,对参数的更新产生了作用:
它与未正则化的模型相比,在于更新
# 2. 为什么正则化可以预防过拟合
# 2.1 例证 1
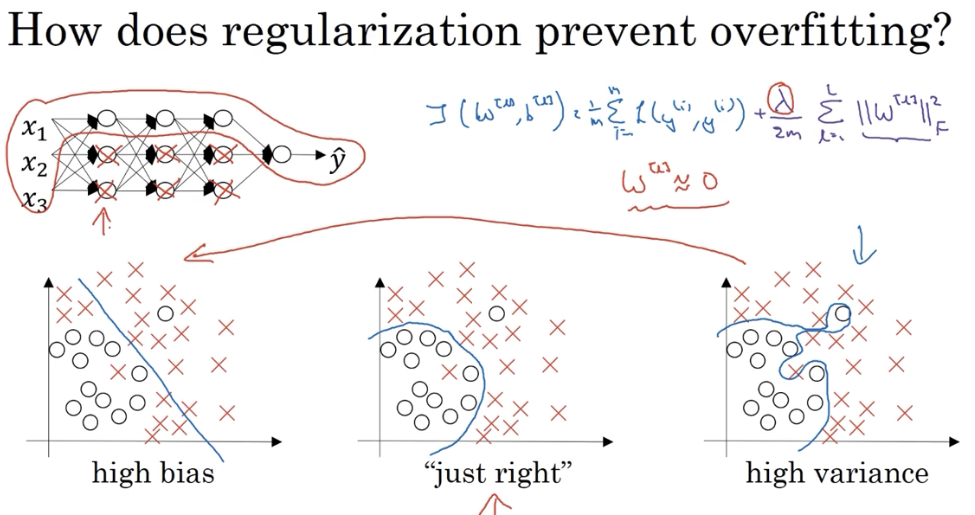
假设未添加正则式之前,模型处于过拟合的状态。在添加正则式之后,如果
直观理解就是正则化使得隐藏层中的许多节点不起作用,变成一个相对简单的模型。节点并未消失,只是没起到作用。
# 2.2 例证 2
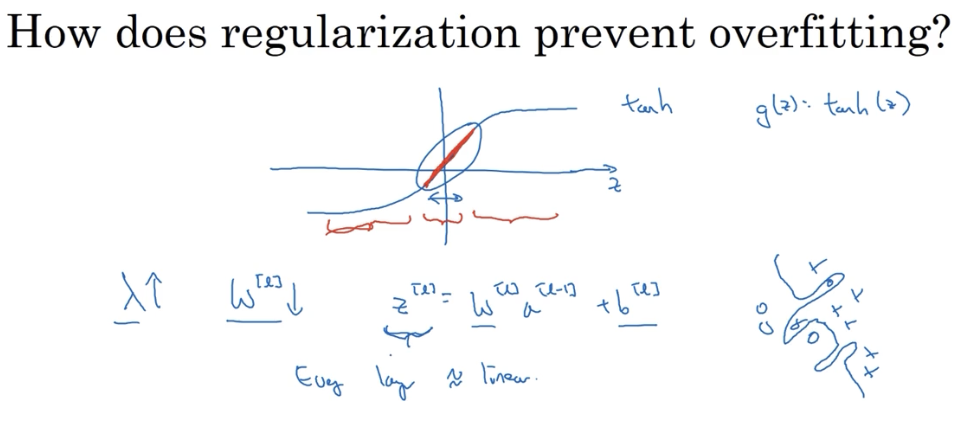
根据正则化后的成本函数,当
根据激活函数的设计,当
# 3. Dropout 正则(随机失活)
# 3.1 思想
Dropout 模型通过在训练时随机删除网络中的神经单元,实现模型的正则化。
对于一个样本的一次训练过程,dropout 会遍历网络的每一层,并设置消除神经网络中节点的概率。得到需要删除的隐藏层节点,然后删掉从该节点进出的连线,最终得到一个节点更少、规模更小的网络。然后使用该样本对网络进行一次训练。
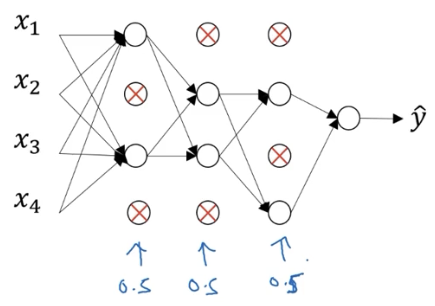
对于其他样本,同样以概率消除节点的方式进行模型精简并训练。
# 3.3 实现
实现 Dropout 正则化有很多方式,这里采用 Inverted dropout 方法实现。
在 foreprop 阶段:

在测试阶段,不使用 Dropout,因为我们不希望测试阶段得到的预测结果是随机的。
# 3.3 理解
一个直观理解是,每次 Dropout 都会使神经网络变成一个更小的网络,因此能够避免过拟合。
通过 Dropout 的训练,神经单元不能依赖任何一个特征或神经单元,因为对方有可能被随机清除,即该神经单元的输入是不稳定的。因此,它不会给任一输入加上过分的权重。
每个神经单元都这样做,权重传播下去,使得 Dropout 产生收缩权重的平方范数的效果。
# 3.4 与 L2 范数的比较
Dropout 正则化实现了类似 L2 正则化的效果,甚至比它的应用范围还要更广。
Dropout 可以为不同隐藏层设置不同的 keep_prob 系数:
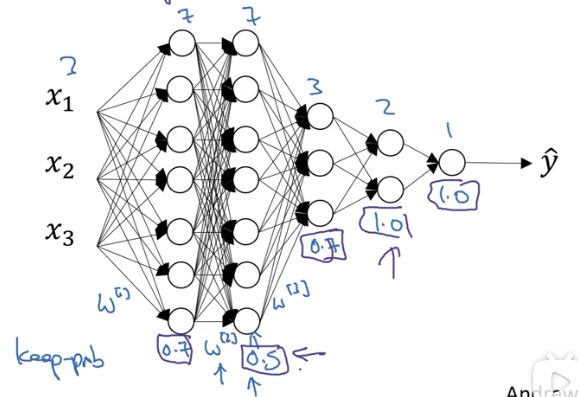
当值为 1 时,表示对该层节点不做随机删除。
使用 Dropout 的一个缺点是,损失函数不再有很明确的定义,对于模型的调试成为问题。最佳实践是先把所有的 keep_prob 设为 1 以关闭 Dropout,跑一遍模型,以确保损失函数是单调递减的。然后再打开 Dropout 进行训练。
# 4. 其他正则化方法
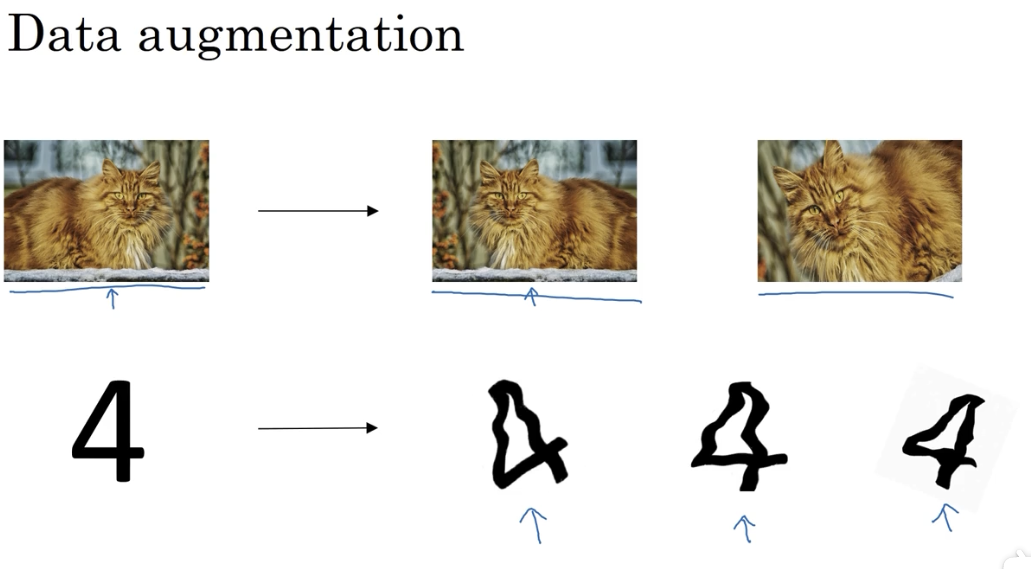
# 4.1 Data augmentation(增加数据)
- 镜像图片
- 随机翻转并裁减
# 4.2 Early stopping
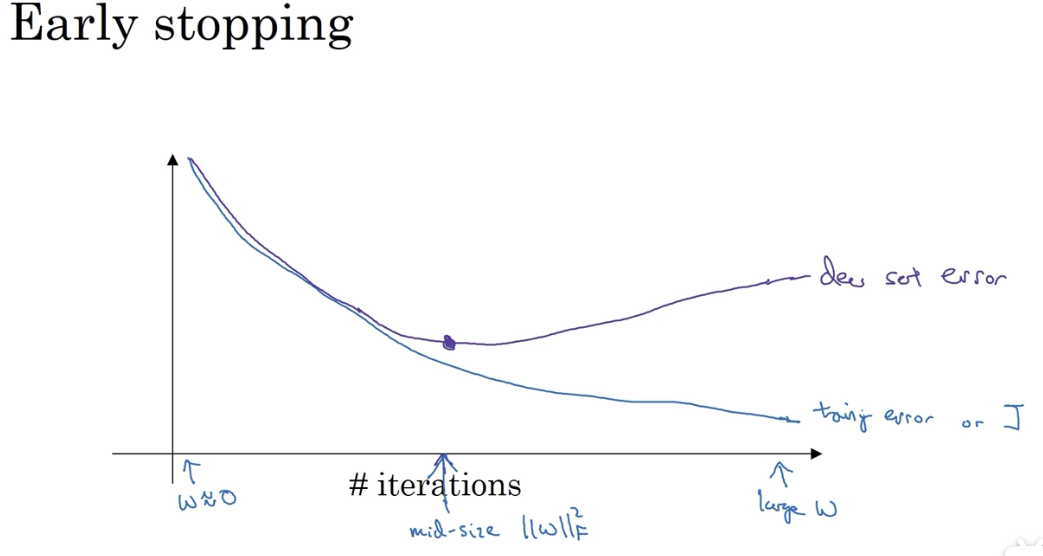
提前终止的一个缺点在于,它虽然避免了过拟合,但它的提前终止也放弃了进一步优化损失函数的可能性。
# 附
深度学习的几个步骤:
- 选择一个算法来优化损失函数
- 梯度下降
- Momentum
- RMSprop
- Adam
- 避免过拟合
- 正则化(会增加超参的选择成本)
- 扩增数据
